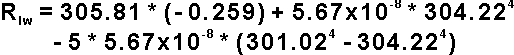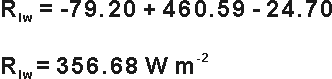One way to calculate the energy output {Wm-2} from Eppley Pyrgeometer (PIR) is to use the temperature of the dome and thermopile thermistors {mV}and the thermopile output {mV} (Albrecht and Cox, 1997).
A. Express thermopile thermistor (TT) and dome thermistor (DT) values in units of volts (Mi)
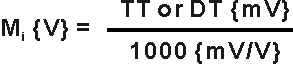
|
(1) |
i = thermopile thermistor (T) or dome thermistor (D)
B. Express thermopile thermistor (TT) and dome thermistor (DT) values (Mi) in terms of resistance (Ri)
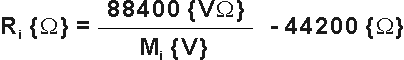
|
(2) |
where
M = thermistor voltage {V}
44200 = resistor resistance {W}
excitation voltage = 2 {V}
88400 = resistor resistance * excitation voltage (VW)
C. Express thermopile and dome thermistor resistance values (Ri) in terms of temperature (i.e.,Tt and Td for thermopile and dome temperatures, respectively)
Use the table below. Interpolate between given values to the nearest hundredth degree.| Temperature vs Resistance for the YSI 44031 Precision Thermistor | |||||
| Temperature (oC) | Resistance (W) | Temperature (oC) | Resistance (W) | Temperature (oC) | Resistance (W) |
| -40 | 239800 | 7 | 21450 | 54 | 3385 |
| -39 | 225000 | 8 | 20520 | 55 | 3270 |
| -38 | 213200 | 9 | 19630 | 56 | 3160 |
| -37 | 201100 | 10 | 18790 | 57 | 3054 |
| -36 | 189600 | 11 | 17980 | 58 | 2952 |
| -35 | 179200 | 12 | 17220 | 59 | 2854 |
| -34 | 169300 | 13 | 16490 | 60 | 2760 |
| -33 | 150000 | 14 | 15790 | 61 | 2669 |
| -32 | 151200 | 15 | 15130 | 62 | 2582 |
| -31 | 143000 | 16 | 14500 | 63 | 2497 |
| -30 | 135200 | 17 | 13900 | 64 | 2417 |
| -29 | 127900 | 18 | 13330 | 65 | 2339 |
| -28 | 121100 | 19 | 12790 | 66 | 2254 |
| -27 | 114600 | 20 | 12260 | 67 | 2191 |
| -26 | 108500 | 21 | 11770 | 68 | 2122 |
| -25 | 102900 | 22 | 11290 | 69 | 2055 |
| -24 | 97490 | 23 | 10840 | 70 | 1990 |
| -23 | 92430 | 24 | 10410 | 71 | 1928 |
| -22 | 87660 | 25 | 10000 | 72 | 1858 |
| -21 | 83150 | 26 | 9605 | 73 | 1810 |
| -20 | 78910 | 27 | 9227 | 74 | 1754 |
| -19 | 74910 | 28 | 8867 | 75 | 1700 |
| -18 | 71100 | 29 | 8523 | 76 | 1648 |
| -17 | 67570 | 30 | 8194 | 77 | 1598 |
| -16 | 64200 | 31 | 7880 | 78 | 1549 |
| -15 | 61020 | 32 | 7579 | 79 | 1503 |
| -14 | 58010 | 33 | 7291 | 80 | 1458 |
| -13 | 55170 | 34 | 7016 | 81 | 1414 |
| -12 | 52480 | 35 | 6752 | 82 | 1372 |
| -11 | 49940 | 36 | 6500 | 83 | 1332 |
| -10 | 47540 | 37 | 6258 | 84 | 1293 |
| -9 | 45270 | 38 | 6026 | 85 | 1255 |
| -8 | 43110 | 39 | 5805 | 86 | 1218 |
| -7 | 41070 | 40 | 5592 | 87 | 1153 |
| -6 | 39140 | 41 | 5389 | 88 | 1149 |
| -5 | 37310 | 42 | 5193 | 89 | 1118 |
| -4 | 35570 | 43 | 5006 | 90 | 1084 |
| -3 | 33930 | 44 | 4827 | 91 | 1053 |
| -2 | 32370 | 45 | 4655 | 92 | 1023 |
| -1 | 30890 | 46 | 4489 | 93 | 994.2 |
| 0 | 29490 | 47 | 4331 | 94 | 956.3 |
| 1 | 28150 | 48 | 4179 | 95 | 939.3 |
| 2 | 26890 | 49 | 4033 | 96 | 913.2 |
| 3 | 25690 | 50 | 3893 | 97 | 857.9 |
| 4 | 24550 | 51 | 3758 | 98 | 853.4 |
| 5 | 23460 | 52 | 3629 | 99 | 839.7 |
| 6 | 22430 | 53 | 3504 | 100 | 815.8 |
D. Calculate longwave radiant flux density according to Albrecht and Cox (1977)
(3) |
where
Rlw = incoming or outgoing irradiance {Wm-2}
C = Calibration Constant {Wm-2mV-1}
E = Thermopile output {mV}
s = Stephan-Boltzman constant = 5.67x10-8 Wm-2K-4
Tt = Thermopile temperature {Kelvin}
Td = Dome temperature {Kelvin}
k = 5
E. References
Albrecht, B. and S.K. Cox. 1977. Procedures for improving pyrgeometer performance, J. of Appl. Meteorol., 16:188-197.F. Example of Calculation
(data from July 17, 1992 at 10:00 am for incoming longwave radiation at Lincoln, NE)Given the values of
thermopile thermistor (TT) = 1657 mV ,
dome thermistor (DT) = 1666 mV,
thermopile output (E) = -0.259 mV and
calibration constant (C) = 305.81 Wm-2mV-1.
Step
|
Thermopile Thermistor
|
Dome Thermister
|
| A. Express in volts {V} |
1.657
|
1.666
|
| B. Express in Resistance {W} |
9149.4267
|
8861.2245
|
| C. Interpolate Resistance to Temperature {C} |
27.22
|
28.02
|
D. Apply to Equation 3